In this post, I discuss my findings on image filtering, specifically how to do trilinear interpolation inside a pixel shader for non-power-of-two textures (npot). The shortcoming is due to the fact that the OpenGL ES 2.0 specification does have a restriction on the wrap modes that can be used if the texture dimensions are non power of two. It only allows CLAMP_TO_EDGE for the wrap mode whereas for the minification filter it only allows for GL_NEAREST or GL_LINEAR. In other words, for npot textures the GLES 2.0 spec doesn't require support for trilinear filtering! GPU vendors, however, are expected to fully support this feature through an extension (i.e., GL_OES_texture_npot) although not required.
In the next sections I explain some of the theory and math behind trilinear filtering followed by my own implementation using the OpenGL ES Shading Language (GLSL). At the end I show some of the screenshots I obtained from the pixel shader.
Texture Mapping
In the next sections I explain some of the theory and math behind trilinear filtering followed by my own implementation using the OpenGL ES Shading Language (GLSL). At the end I show some of the screenshots I obtained from the pixel shader.
Texture Mapping
In real-time 3D Graphics objects are modeled in 3D space and images are mapped onto the faces of the objects. This not only add some realism to the scene, the GPU can do it quite inexpensively. The image data is loaded and gets converted into a 2D array where individual data elements are called texture elements or texels. When rendering with a 2D texture, a texture coordinate is used as an index into the texture image, and then mapped to the destination image (screen) by the viewing projection. Texture space is labeled (s, t) and screen space is labeled (x, y).
 |
| Figure 1. Pixel mapping to texture-space. Figure taken from [1]. |
When the texture gets resized (i.e., minimized) a visual artifact called aliasing might suddenly appear in the final image. This happens because as the geometry gets smaller and smaller the texture coordinates take large jumps when being interpolated from pixel to pixel. Thus, aliasing occurs when not enough samples are preserved from the original image that the final image looks jagged or pixelated. There are several texture filtering techniques that smoothly blend or interpolate adjacent pixels in order to avoid aliasing. The most common ones are bi-linear interpolation, trilinear interpolation (or mipmapping) and anisotropic filtering.
Texture Filtering
"Heckbert [12] defined texture filtering as the process of re-sampling the texture image onto the screen grid", Ewins et al [1]. Each screen coordinate (x, y) maps to a texture-space coordinate (s, t) as shown in Figure 1 above. The job of the texture filtering mechanism is then to efficiently determine which texel in the texture map correspond to what pixel in the screen. Since performing texture look-ups involves accessing texture memory this is in turn a time consuming operation", Ewins et al [1]. For this reason mipmaps (a filtering technique) was developed in order to reduce memory accesses since it relies on pre-filtered texture storage.
Mipmaps
The idea behind mipmaps is to generate a pyramid of textures, each level in the pyramid representing a level of detail l that hints the GPU where to sample from during texture minification. Each of the levels in the pyramid are exactly a scaled down version of the original texture in both dimensions. For example, if the original texture is 256 x 256 in size the next scaled down version would be 128 x 128 and so forth all the way down to 1 x 1 texel. Mipmapping helps with aliasing because thanks to the many levels that the GPU can now sample from the pixel to texel ratio is better preserved. More over, since now the texture fetches happen at a relative closer distance (the map is smaller) the GPU can better utilize the cache thus improving performance when using mipmapping over other filtering methods that doesn't. A clear disadvantage for mipmapping is that it requires extra storage space for all the additional levels.
 |
| Figure 2. Mipmap pyramid. Figure taken from [1]. |
The mechanism by which the GPU calculates the level of detail is not important. What's important is to be able to sample the different levels inside the pixel shader, and to do that we need to somehow calculate this number ourselves. In the next section I go over an approximation that has been discussed before that can help us determine the level of detail inside the shader. Once the level of detail is known, we then take two bilinear samples, one at the calculated level and the other one at the level below it. Finally, we return the color by doing a third linear-interpolation between these two levels to have trilinear interpolation.
Mipmap Level Selection
It's very common in Computer Graphics to represent a pixel as square. Building upon that one can roughly approximate a texture map as a parallelogram in texture space, see Figure 3. The mapping of the texels (s,t) in texture space with respect of the pixels (x,y) in screen space can be approximated using partial derivatives according to [1].
The vector length of both r1 and r2 can be calculated as
We then choose the level of detail based on the maximum compression of an edge in texture space, which corresponds to the maximum length of either side of the parallelogram in texture space:
We know a pixel at a level l covers an area,
For a parallelogram of a given area A, we can approximate its area by
where the area (A) is then replaced by Eq3 above to approximate the level of detail.
It's very common in Computer Graphics to represent a pixel as square. Building upon that one can roughly approximate a texture map as a parallelogram in texture space, see Figure 3. The mapping of the texels (s,t) in texture space with respect of the pixels (x,y) in screen space can be approximated using partial derivatives according to [1].
 |
| Figure 3. Pixel mapping to texture-space using constant partial derivatives. Figure taken from [1]. |
The vector length of both r1 and r2 can be calculated as
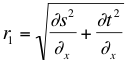 |
| Eq1: Vector length r1 |
 |
| Eq2: Vector length r2 |
 |
| Eq3: Maximum length of either side of parallelogram |
We know a pixel at a level l covers an area,
For a parallelogram of a given area A, we can approximate its area by
 |
| Eq4: Level of detail in terms of pixel area |
Implementation
The implementation was written using the OpenGL ES Shading Language as found in any Open GL ES 2.0 implementation. It however, rely on two shader extensions that may or may not be supported in all hardware implementations out there. The first of this extensions is called GL_OES_standard_derivatives which give us the ability to calculate derivatives.
The second of the required extensions is called GL_EXT_shader_texture_lod and adds additional texture functions to the Shading Language allowing us to have explicit control of the level of details inside the mipmap pyramids. In other words, we can explicitly define which texture level to sample from.
Both of these extensions can only be used inside fragment shaders.
The implementation was written using the OpenGL ES Shading Language as found in any Open GL ES 2.0 implementation. It however, rely on two shader extensions that may or may not be supported in all hardware implementations out there. The first of this extensions is called GL_OES_standard_derivatives which give us the ability to calculate derivatives.
#extension GL_OES_standard_derivatives : enable
The second of the required extensions is called GL_EXT_shader_texture_lod and adds additional texture functions to the Shading Language allowing us to have explicit control of the level of details inside the mipmap pyramids. In other words, we can explicitly define which texture level to sample from.
#extension GL_EXT_shader_texture_lod : enable
Both of these extensions can only be used inside fragment shaders.
float mipmapLevel(vec2 uv, vec2 textureSize)
{
//rate of change of the pixels in u and v with respect to window space
//approximate to au/ax, au/ay, av/ax, av/ay
vec2 dx = dFdx( uv * textureSize.x);
vec2 dy = dFdy( uv * textureSize.y);
//select the LOD based on the maximum compression of an edge in texture space.
//This corresponds to the maximum length of a side in texture space
//max (sqrt(dUdx*dUdx + dVdx*dVdx),
// sqrt(dUdy*dUdy + dVdy*dVdy));
float d = max( dot (dx, dx), dot( dy, dy));
//convert d length to power-of-two level of detail
return 0.5*log2(d);
}
vec4 texture2D_trilinear( sampler2D tex, vec2 uv)
{
float level= mipmapLevel(uv, u_texsize);
//sample the current level
vec4 t00 = texture2DLodEXT(tex, fract(uv), level);
//sample the level directly below it
vec4 t01 = texture2DLodEXT(tex, fract(uv), level+1.);
//linear interpolate the two levels
return mix(t00, t01, fract(level));
}
void main()
{
gl_FragColor = texture2D_trilinear( colorMap, v_texCoord.st);
}
First we start with the mipmapLevel() function. In this function we use the derivatives to figure out the rate of change of the texture coordinates (u,v) with respect to screen coordinates. Note that since we are interested in non-power-of-two textures we need to scale up the partial derivatives by the texture dimensions in both x and y. For this I just use a uniform u_texsize that contains the texture dimensions. We then calculate the maximum value of the two edges in the parallelogram and simply return the base 2 log() of this length.
After we figure out the level of detail we are then ready to start sampling from the mipmap levels. From the application in GL we set the minification filters to GL_LINEAR_MIPMAP_NEAREST in order to take a bilinear fetch from the closet mip level chosen. After fetching from the two levels that we are interested in we return the color by doing one last linear interpolation to give us a trilinear filtering.
Note that the level of detail is calculated as a real number (l = 0.f) where the fraction (f) is being used as the weight factor in the linear interpolation, see Figure 2 above. This is done to produce a smooth linear blend between the levels.
Results
References
[1] Ewins JP, Waller MD, White M, Lister PF. MIP-map level selection for texture mapping. IEEE Transactions on Visualization and Computer Graphics 1998. Available online.
[2] J.P. Ewins, M.D. Waller, M. White, and P.F. Lister, “An Implementation of an Anisotropic Texture Filter,” Technical Report IWD_172, Centre for VLSI and Computer Graphics, Univ. of Sussex, 1998. Available online.
[3] Munshi, Aartab; Ginsburg, Dan; Shreiner, Dave. OpenGL ES 2.0 Programming Guide. Addison-Wesley Professional.
[4] Gerasimov, Phillip, Randima, Fernando, Green, Simon. "Shader Model 3.0: Using Vertex Textures." NVIDIA white paper, June 2004. Available online.
[5] Marschner, Steve. "Texture filtering" CS 4620 Lecture notes, Fall 2008, Cornell University. Available online.
[6] Guinot, Jerome. "The art of texturing Using the OpenGL Shading Language". April 15, 2006. Available online.
[7] Flavell, Andrew. "Run-Time MIP-Map Filtering". December 11, 1998. Available online.
No comments:
Post a Comment